Noviembre

01 de noviembre del 2016

Clase 5 

RECTA DETERMINADA POR DOS PLANOS:

Como se indico en la clase anterior se pueden determinar varios elementos a partir de una interseccion entre dos planos asi como son rectas y se las puede obtener basandose en varias ecuaciones generales:

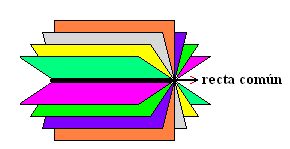
HAZ DE PLANOS:
El haz de planos es un conjunto infinito de planos unidos uno tras otro de manera que sus generatrices son paralelas como se indica en el grafico.

 

Pueden determinarse sus puntos, y la distancia entre cada extremo de cada plano o superficie de manera general con una ecuacion:

DISTANCIA DE UN PUNTO A UNA RECTA:

Para encontrar la distancia existente entre un punto y una recta se aplica una ecuacion que esta en funcion de las coordenadas del punto como un lado del plano.

ECUACION VECTORIAL DE LA ESFERA:

Para hallar esta ecuación se necesita conocer  varios elementos de la esfera, se debe conocer tanto la ubicacion del centro de la esfera asi como tambien su radio de manera que sea posible reemplazar cada dato en una ecuacion general de analisis.

08 de noviembre del 2016

Clase 6 

SUPERFICES DE SEFUNDO GRADO (CUADRICAS):

Son llamadas asi las superficies que han sido determinadas por ecuaciones de seunto grado pero en el espacio tridimencional y pueden ser representadas con una ecuacion similar a la siguiente:

Para analizar estas superficies se realizan tres pasos de manera ordenada y son:

        1. Intersección con los ejes coordenados: OX; OY; OZ.
       2. Intersección con los planos coordenado: XOY; XOZ; YOZ.

       3. Intersección con los planos paralelos a los planos coordenados: XOY; XOZ; YOZ

Despues de estos tres pasos indispensables se realiza un cuarto paso para tener una mejor idea de lo que se analiza: 

       4. Bosquejo de la gráfica de la superficie.

Las superficies cuadricas que se generan  mas comunmente y tiene  un analisis propio son las presentadas a ontinuacion:

15 de noviembre del 2016

Clase 7

FUNCIONES VECTORIALES: 

Con el esquema presentado se pueden determinar varios factores de las funciones como por ejemplo que las funciones vectoriales pueden tener "n" componentes: F(t) = (f1(t), f2(t), ....... fn(t)) pero como nuestro campo de trabajo es R3, se utilizan unicamente 3 componentes que nos dan 3 dimenciones y se epresentan asi:  r(t) = ( f(t), g(t), h(t) )

La Ecuacion Cartesiana de la Curva dada por la Ecuacion principal puede ser obtenida al eliminar el parametro (t).

OPERACIONES CON FUNCIONES VECTORIALES:  

Dadas dos funciones vectoriales se pueden realizar distintas  operaciones similares a las operaciones entre vectores como:

18 de noviembre del 2016

Clase 8

LIMITES, CONTINUIDAD Y DERIVACION:

EL LIMITE:

El límite de f(x) cuando x tiende a x₀ es igual a L si y sólo si para todo número real mayor que cero existe un número real δ mayor que cero tal que si la distancia entre x y x₀ es menor que δ, entonces la distancia entre la imagen de x y L es menor que ε".

Se escribe:

Lim _t—t0 f (t) = A

Si A vector = (a1, a2,……a_n) se prueba que: lim _t—& f_i (t) = a_i

Ɐ _i = 1, 2,3…..n

OBSERVACION:

• Dada la función F  de I en R^n, donde F (t)= (f1 (t), f2 (t)….fn (t)); si una de ellas no tiene límite no existe límite de la función

CONTINUIDAD:

Para la continuidad sea F de I a Rⁿ y sea t₀ pertenece a I se dice que F (t) es continua en t=to, si:

Lim _t—t0 F (t) = F (to)

OBSERVACION:

• Si F de I en  Rⁿ, donde: F (t)= (f1 (t), f2 (t)….fn (t)), es continua en to, entonces

Lim _t—t0 F (t) = F (to) ↔ lim _t—t0 f_i (t) = f_i (to)              i= 1, 2, 3…..n

DERIVACIÓN:

En la definicion de derivacion dada F de I a Rⁿ, I pertenece a R y sea t0 pertenece a I, se dice que: F (t) es derivable en t0 si existe:

INTEGRACION:

La integral definida de una función vectorial continua se define de forma similar a la integral de una función con valores reales, pero teniendo en cuenta que ahora el resultado es un vector y es una accion contraria a la derivacion..

PROPIEDADES DE LA INTEGRACION:

22 de noviembre del 2016

Clase 9

VELOCIDAD Y ACELERACION

VECTORES TANGENTE UNITARIO Y NORMAL PRINCIPAL

VECTOR TANGENTE UNITARIO 

La tangente de una curva es una recta que intersecta la curva en un solo punto. Es conocido por nosotros a través del cálculo que mediante la diferenciación de una función se obtiene el punto tangencial para la curva de esa función. Un concepto similar es aplicable al cálculo vectorial, junto con una excepción.

Para una función con un vector de la forma, (x), un vector de la forma es llamado vector tangente en el caso de que esta función sea real y su magnitud no sea igual a cero. En esta situación, la tangente de la función dada (x) en un punto arbitrario es paralela al vector tangente, en ese punto. Aquí, con el fin de tener un vector tangente, 0 es un pre-requisito esencial. Esto es debido a que un vector de magnitud cero no puede tener dirección.

PLANO OSCULADOR

Si n= 3

El plano osculador, pasa por el punto F (t) y esta generado por T (t) y N (t), tangente y normal. Es l plano que mejor se ajusta  a la curva en una velocidad de F

n= (Bx, By, Bz);  p (xo, yo, zo)

Bx (x- xo) +By (y- yo) +Bz (z- zo) = 0

PLANO NORMAL

Se forma entre el vector  normal y binomial

T = (Tx, Ty, Tz);  p (x0, y0, z0)

Tx (x- xo) +Ty (y- yo) + Tz (z- zo) = 0

PLANO RECTIFICANTE

Se forma entre el actor tangente y el binomial

N= (Nx, Ny, Nz)    p (xo, yo, zo)

Nx (x- xo) + Ny (y- yo) + Nz (z- zo)

RECTA TANGENTE

La recta tangente es la recta que pasa por el vector tangente

a= T (t) = (Tx, Ty, Tz)

r= ro + t (Tx, Ty, Tz)

x= xo + tTx

y= yo + tTy

z= zo + tTz

RECTA NORMAL PRINCIPAL

La recta normal principal es la recta que pasa sobre el vector normal

a= N (t) = (Nx, Ny, Nz)

r= ro + t (Nx, Ny, Nz)

x= xo + tNx

y= yo + tNy

z= zo + tNz

RECTA BINOMIA

La recta que pasa por el vector binomial

a= B (t) = (Bx, By, Bz)

r= ro + t (Bx, By, Bz)

x= xo + tBx

y= yo + tBy

z= zo + tBz

VECTOR CURVATURA

La medida en la cual se desvía un determinado objeto geométrico se conoce como curvatura. Existen básicamente dos tipos principales de curvatura: curvatura intrínseca y extrínseca. Para los objetos que se encuentran en un espacio diferente, en este tipo de enfoque que se relaciona con la curvatura del radio del círculo que traza el objeto correspondiente, se define una curvatura extrínseca. El círculo puede ser el ejemplo más sencillo de una curvatura extrínseca dado que encada punto de la circunferencia; la curvatura es igual al recíproco del radio. La curvatura intrínseca en la naturaleza es descrita por la variedad de Riemann en cada punto.

Una curvatura en un plano pertenece a una cantidad escalar, mientras que en 2D o 3D, la identidad de la curvatura es definida como un vector en el cual tanto la nitidez como la dirección de inclinación es considerada.

25 de noviembre del 2016

Clase 10

FUNCIONES REALES DE ARGUMENTO VECTORIAL:

• Si f(x,y)= z la gráfica en el espacio se obtiene una superficie
• El dominio de la funcion f(x,y) es un conjunto de escalares z elementos del espacio.
• El rango de la función f(x,y) es un conjunto de escalares z elemento del espacio.
• La gráfica de f(x,y,z)=w no se puede representar en el espacio, pero sería una hipersuperficie. Solo se puede obtener el dominio de la función.

Para determinar el dominio dela función se debe realizar un análisis:

• Analítico (Matemáticamente)
• Gráfico
• Descriptivo

En el siguiente video se puede visualizar un claro ejemplo sobre este tema:

Sea D un subconjunto en Rn, se dice que f es una función real de argumento vectorial, si a cada elemento  x (x1, x2, x3, .... xn) le corresponde un único valor real de z

Se puede obtener el dominio y el rango de estas funciones

•   Para hallar el Dominio de la Función es recomendable analizarlo de tres maneras de manera analitica, gráfica y descritiva.

APLICACIÓN DE LAS FUNCIONES REALES

1. se aplican estas funciones para explicar fenomenos naturales como la Temperatura de la Tierra en función de la longitud y latitud
2. La Temperatura de una placa o lámina en funcion de la posición (x,y)
3. Las funciones de la densidad o distribución de masa f(x,y,z), que dependen de el largo, ancho y altura 
4. Incluso se puede expresar costos, la función  costos c=f (x,y) donde este dependerá de costos fijos y costos variables. 

CURVAS DE NIVEL

Se define como curvas de nivel a  el conjunto de  todos los puntos del plano donde f (x,y) tiene un valor constante, es decir f (x,y)=c, y se llama CURVA DE NIVEL DE F.

29 de noviembre del 2016

Clase 11 

LIMITES Y CONTINUIDAD:Para funciones de una sola variable, cuando dejamos que x se aproxime a a, sólo hay dos posibles direcciones de acercamiento, por la izquierda o por la derecha. Para funciones de dos variables, la situación no es tan sencilla, puesto que podemos dejar que (x, y) se aproxime para una función de dos variables:

tal que:

El entorno de aproximación es un disco de centros (a,b) y de radios d (d>0)

Se tienen infinitos caminos de aproximación a (a,b) por tanto:

• si por dos caminos o trayectorias diferentes el valor del limite es diferente, entonces concluimos que el limite no existe
• si por dos o mas caminos el valor del limite es el mismo, suponemos que el limite existe y debemos proceder a demostrar su existencia

En esta clase se estudio como demostrar la existencia del limite que se puede hacer por dos formas:

• Coordenadas polares: que consiste en realizar un cambio de variable donde:

Por medio de la definición

• Para calcular el límite de una función f(x,y) se debe reducir al limite de una variable.
• Existen infinitos caminos o trayectorias de acercamiento a (a, b).
• Si por dos caminos el valor del límite tiene valores diferentes, entonces se concluye que no existe el límite.
• Si por dos o más caminos diferentes el valor del límite tiene igual valor, se debe demostrar con la definición u otro método.

CONTINUIDAD: Para determinar la continuidad de una función en un punto P, se debe verificar que: El limite debe existir f(x₀,y₀); si el limite existe f(x,y)este debe tender a cero; necesariamente el limite f(x₀,y₀) = limite f(x,y).
Función discontinua evitable (redefinible)

•       El limite debe existir f(x₀,y_0).
•       Si el limite existe f(x,y)este debe tender a cero.
•       No Necesariamente el limite f(x₀,y₀) = limite f(x,y).

Función discontinua inevitable

•  El límite de la función en ese punto no existe