Febrero

03 de Febrero del 2017                                                                

Clase 25

Rotacional:

Se entiende por rotacional al operador vectorial que muestra la tendencia de un campo a inducir rotación alrededor de un punto. También se define como la circulación del vector sobre un camino cerrado del borde de un área con dirección normal a ella misma cuando el área tiende a cero (Ecuación 1).

(1)

Aquí, S es el área de la superficie apoyada en la curva C , que se reduce a un punto. El resultado de este límite no es el rotacional completo (que es un vector), sino solo su componente según la dirección normal a S y orientada según la regla de la mano derecha. Para obtener el rotacional completo deberán calcularse tres límites, considerando tres curvas situadas en planos perpendiculares.

El rotacional de un campo se puede calcular siempre y cuando este sea continuo y diferenciable en todos sus puntos.

El resultado del rotacional es otro campo vectorial que viene dado por el determinante de la siguiente ecuación:

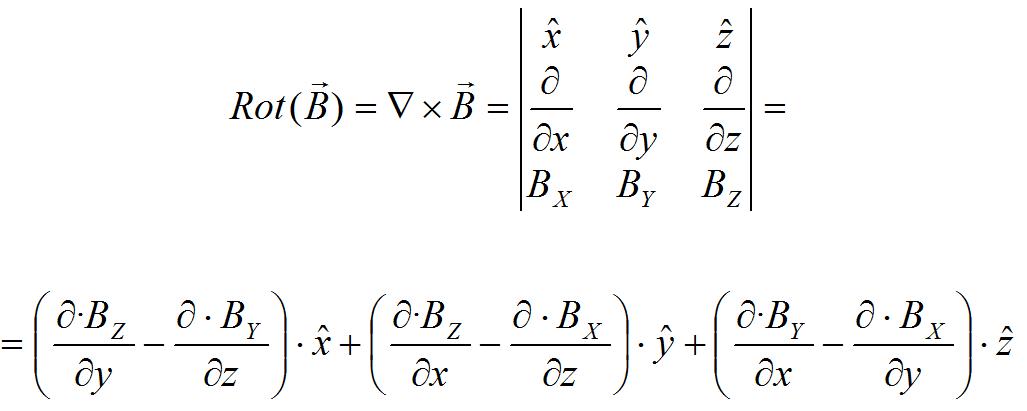(2)

Las propiedades más destacadas del rotacional de un campo son:

•  Si el campo escalar f(x,y,z) tiene derivadas parciales continuas de segundo orden entonces el rot (f) =0

•  Si F(x,y,z) es un campo vectorial conservativo entonces rot (F) = 0

•  Si el campo vectorial F(x,y,z) es una función definida sobre todo  cuyas componentes tienen derivadas parciales continuas y el rot (F) = 0, entonces F es un campo vectorial conservativo.

Operador laplaciano:

En calculo vectorial, el operador laplaciano o laplaciano es un operqador difercial elíptico de segundo orden, denotado como Δ, relacionado con ciertos problemas de minimización de ciertas magnitudes sobre un cierto dominio. 

Expresado en coordenadas cartesianas es igual a la suma de todas las segundas derivadas parciales no mixtas dependientes de una variable. Corresponde a diy (grad φ), de donde el uso del símbolo delta (Δ) o nabla cuadrado (${\displaystyle \nabla ^{2}}$) para representarlo. Si ${\displaystyle \phi ,\mathbf {A} }$, son un campo escalar y un campo vectorial respectivamente, el laplaciano de ambos puede escribirse en términos del operador nabla como:

${\displaystyle \Delta \phi =(\nabla \cdot \nabla )\phi =\nabla ^{2}\phi \qquad \qquad \Delta \mathbf {A} =\nabla (\nabla \cdot \mathbf {A} )-\nabla \times (\nabla \times \mathbf {A} )=(\nabla \cdot \nabla )\mathbf {A} }$

07 de Febrero del 2017                                                                

Clase 26

MASA DE UN ALAMBRE.

La interpretación física que se le pueda dar a la integral de línea ∫c f(x,y) ds  dependerá del significado físico que tenga la función f. Si la función ρ (x, y) representa la densidad lineal de un punto (x, y) de un alambre muy delgado en forma de la curva C y si se divide la curva C en n subarcos de longitudes  ∆s1,∆s2,∆s3,…..,∆sn , con  ∆sf ≈ (Pi-1 Pi), entonces la masa del alambre que va desde Pi−1 hasta  Pi se puede aproximar mediante la siguiente expresión ρ (xi*,yi*) ∆si ; por  tanto la masa del alambre completo vendría dado por ∑ni-1 (ρ (xi*,yi*) ∆si). Para tener una aproximación más cercana al valor verdadero de la masa del alambre se puede  incrementar el número de subarcos n en el que se dividió inicialmente la curva C. Al estudiar el límite de estas aproximaciones cuando n → ∞, se obtiene el valor exacto de la masa del alambre:

M = limn → ∞∑ni-1 (ρ (xi*,yi*) ∆si) = ∫c f(x,y) ds  

Para elementos como espirales, muelles o alambres cuya densidad lineal puede ser  variable, la integral de línea permite el cálculo de la masa de estos elementos  apoyados en la definición de la misma con respecto a la longitud de arco, como se observará en los siguientes ejemplos.

EJEMPLOS:

1) Hallar la masa de un alambre formado por la intersección de la superficie esférica X2+Y2+Z2=1, y el plano x+y+z = 0, si la densidad en (x,y,z) está dada por  ρ (x,y,z) = X2 gramos por unidad de longitud del alambre.

10 de Febrero del 2017                                                                

Clase 27

17 de Febrero del 2017                                                                

Clase 28

Desplazamiento de la trayectoria

En la dinámica del punto material, se entiende por desplazamiento el vector o segmento recto orientado que une la posición inicial con otro punto genérico de la trayectoria. Este uso del vector desplazamiento permite describir en forma completa el movimiento y el camino de una partícula.

Cuando el punto de referencia es la posición previa de la partícula, el vector desplazamiento indica la dirección del movimiento por medio de un vector que va desde la posición previa a la posición actual. Este uso del vector desplazamiento es útil para definir a los vectores velocidad y aceleración de una partícula definida.

El teorema fundamental de las integrales de linea:

donde  es continua en . El teorema del cambio total también se llama ecuación 1, La integral de una razón de cambio es el cambio total.

Si pensamos que el valor gradiente  de una función  de dos ó tres variables es una especie de derivada de , entonces el teorema siguiente puede considerarse como una versión del Teorema Fundamental para las Integrales de Línea.

Teorema:

Sea una Curva C una curva suave dada por la función vectorial . Sea "f" una función derivable de dos ó tres variables, cuyo vector gradiente  es continuo sobre C.

Entonces:

El teorema nos dice que podemos evaluar la integral de línea de un campo vectorial conservativo ( el campo vectorial gradiente de la función potencial f) con solo conocer el valor de "f" en los extremos de C. De hecho el teorema nos expresa que la integral de línea de  es el cambio total de "f". Si "f" es una función de dos variables y C es una curva plana con punto inicial A(X1, Y1) y punto final B(X2 , Y2), entonces el teorema se convierte en:

Si "f" es una función de tres variables y C es una curva en el espacio que une  con  , entonces tenemos:

21 de Febrero del 2017                                                                

Clase 29

Teorema de Green

Ejemplos:

22 de Febrero del 2017                                                                

Clase 30

Trabajo en integrales de linea:

La definición más elemental del trabajo es aquella que se da cuando una fuerza constante actúa sobre una partícula, mientras esta se desplaza según una trayectoria plana a lo largo de la línea de acción de la fuerza.

La integral de línea de una fuerza sobre una trayectoria es igual al trabajo realizado por esa dicha fuerza.

                                  

                                          W=∫C F.dr

Sea F(x,y,z) un campo de fuerzas continuo, definido sobre los puntos de una curva acotada C, el trabajo

realizado por el campo de fuerzas F para mover una partícula a lo largo de una curva C de Rn regular a trozos y parametrizada por medio de α está determinado por:

Donde:  es un vector tangente unitario a C que representa la dirección en el cual se aplica la fuerza.